初始化与前四个问题
Signed-off-by: szdytom <szdytom@163.com>
This commit is contained in:
commit
afc6b6349d
2
.gitignore
vendored
Normal file
2
.gitignore
vendored
Normal file
@ -0,0 +1,2 @@
|
|||||||
|
*.pdf
|
||||||
|
*.exe
|
||||||
44
assets/p4-bipart.svg
Normal file
44
assets/p4-bipart.svg
Normal file
@ -0,0 +1,44 @@
|
|||||||
|
<?xml version="1.0" encoding="UTF-8"?>
|
||||||
|
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" width="540pt" height="422pt" viewBox="0 0 540 422" version="1.1">
|
||||||
|
<defs>
|
||||||
|
<clipPath id="clip1">
|
||||||
|
<path d="M 457 339 L 540 339 L 540 421.441406 L 457 421.441406 Z M 457 339 "/>
|
||||||
|
</clipPath>
|
||||||
|
</defs>
|
||||||
|
<g id="surface11">
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 331.398438 L 482.253906 384.464844 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 325.554688 L 482.253906 272.492188 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 56.425781 320.203125 L 483.574219 160.023438 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 54.34375 315.988281 L 485.65625 46.421875 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 483.574219 379.113281 L 56.425781 218.933594 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 485.65625 374.898438 L 54.34375 105.328125 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 266.644531 L 57.746094 213.582031 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 483.574219 261.292969 L 56.425781 101.113281 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 154.671875 L 57.746094 207.734375 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 148.828125 L 57.746094 95.761719 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 483.574219 42.207031 L 56.425781 202.386719 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:butt;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 36.855469 L 57.746094 89.917969 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 384.464844 Z M 482.253906 384.464844 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 482.253906 272.492188 Z M 482.253906 272.492188 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 483.574219 160.023438 Z M 483.574219 160.023438 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 485.65625 46.421875 Z M 485.65625 46.421875 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 56.425781 218.933594 Z M 56.425781 218.933594 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 54.34375 105.328125 Z M 54.34375 105.328125 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 213.582031 Z M 57.746094 213.582031 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 56.425781 101.113281 Z M 56.425781 101.113281 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 207.734375 Z M 57.746094 207.734375 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 95.761719 Z M 57.746094 95.761719 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 56.425781 202.386719 Z M 56.425781 202.386719 "/>
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.746094 89.917969 Z M 57.746094 89.917969 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.925781 328.476563 C 57.925781 322.226563 55.445313 316.234375 51.027344 311.816406 C 46.605469 307.394531 40.613281 304.914063 34.363281 304.914063 C 28.113281 304.914063 22.121094 307.394531 17.703125 311.816406 C 13.28125 316.234375 10.800781 322.226563 10.800781 328.476563 C 10.800781 334.726563 13.28125 340.71875 17.703125 345.140625 C 22.121094 349.558594 28.113281 352.039063 34.363281 352.039063 C 40.613281 352.039063 46.605469 349.558594 51.027344 345.140625 C 55.445313 340.71875 57.925781 334.726563 57.925781 328.476563 Z M 57.925781 328.476563 "/>
|
||||||
|
<path style=" stroke:none;fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;" d="M 529.199219 387.386719 C 529.199219 381.136719 526.71875 375.144531 522.296875 370.722656 C 517.878906 366.304688 511.886719 363.824219 505.636719 363.824219 C 499.386719 363.824219 493.394531 366.304688 488.972656 370.722656 C 484.554688 375.144531 482.074219 381.136719 482.074219 387.386719 C 482.074219 393.636719 484.554688 399.628906 488.972656 404.046875 C 493.394531 408.46875 499.386719 410.949219 505.636719 410.949219 C 511.886719 410.949219 517.878906 408.46875 522.296875 404.046875 C 526.71875 399.628906 529.199219 393.636719 529.199219 387.386719 Z M 529.199219 387.386719 "/>
|
||||||
|
<g clip-path="url(#clip1)" clip-rule="nonzero">
|
||||||
|
<path style="fill:none;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 529.199219 387.386719 C 529.199219 381.136719 526.71875 375.144531 522.296875 370.722656 C 517.878906 366.304688 511.886719 363.824219 505.636719 363.824219 C 499.386719 363.824219 493.394531 366.304688 488.972656 370.722656 C 484.554688 375.144531 482.074219 381.136719 482.074219 387.386719 C 482.074219 393.636719 484.554688 399.628906 488.972656 404.046875 C 493.394531 408.46875 499.386719 410.949219 505.636719 410.949219 C 511.886719 410.949219 517.878906 408.46875 522.296875 404.046875 C 526.71875 399.628906 529.199219 393.636719 529.199219 387.386719 Z M 529.199219 387.386719 "/>
|
||||||
|
</g>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 529.199219 269.566406 C 529.199219 263.320313 526.71875 257.324219 522.296875 252.90625 C 517.878906 248.488281 511.886719 246.003906 505.636719 246.003906 C 499.386719 246.003906 493.394531 248.488281 488.972656 252.90625 C 484.554688 257.324219 482.074219 263.320313 482.074219 269.566406 C 482.074219 275.816406 484.554688 281.8125 488.972656 286.230469 C 493.394531 290.648438 499.386719 293.132813 505.636719 293.132813 C 511.886719 293.132813 517.878906 290.648438 522.296875 286.230469 C 526.71875 281.8125 529.199219 275.816406 529.199219 269.566406 Z M 529.199219 269.566406 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 529.199219 151.75 C 529.199219 145.5 526.71875 139.507813 522.296875 135.085938 C 517.878906 130.667969 511.886719 128.1875 505.636719 128.1875 C 499.386719 128.1875 493.394531 130.667969 488.972656 135.085938 C 484.554688 139.507813 482.074219 145.5 482.074219 151.75 C 482.074219 158 484.554688 163.992188 488.972656 168.410156 C 493.394531 172.832031 499.386719 175.3125 505.636719 175.3125 C 511.886719 175.3125 517.878906 172.832031 522.296875 168.410156 C 526.71875 163.992188 529.199219 158 529.199219 151.75 Z M 529.199219 151.75 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 529.199219 33.929688 C 529.199219 27.683594 526.71875 21.6875 522.296875 17.269531 C 517.878906 12.851563 511.886719 10.367188 505.636719 10.367188 C 499.386719 10.367188 493.394531 12.851563 488.972656 17.269531 C 484.554688 21.6875 482.074219 27.683594 482.074219 33.929688 C 482.074219 40.179688 484.554688 46.175781 488.972656 50.59375 C 493.394531 55.011719 499.386719 57.496094 505.636719 57.496094 C 511.886719 57.496094 517.878906 55.011719 522.296875 50.59375 C 526.71875 46.175781 529.199219 40.179688 529.199219 33.929688 Z M 529.199219 33.929688 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.925781 210.660156 C 57.925781 204.410156 55.445313 198.414063 51.027344 193.996094 C 46.605469 189.578125 40.613281 187.09375 34.363281 187.09375 C 28.113281 187.09375 22.121094 189.578125 17.703125 193.996094 C 13.28125 198.414063 10.800781 204.410156 10.800781 210.660156 C 10.800781 216.910156 13.28125 222.902344 17.703125 227.320313 C 22.121094 231.738281 28.113281 234.222656 34.363281 234.222656 C 40.613281 234.222656 46.605469 231.738281 51.027344 227.320313 C 55.445313 222.902344 57.925781 216.910156 57.925781 210.660156 Z M 57.925781 210.660156 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:rgb(16.078186%,71.37146%,96.469116%);fill-opacity:1;stroke-width:5.4;stroke-linecap:square;stroke-linejoin:miter;stroke:rgb(38.038635%,38.038635%,38.038635%);stroke-miterlimit:3.25;" d="M 57.925781 92.839844 C 57.925781 86.589844 55.445313 80.597656 51.027344 76.179688 C 46.605469 71.757813 40.613281 69.277344 34.363281 69.277344 C 28.113281 69.277344 22.121094 71.757813 17.703125 76.179688 C 13.28125 80.597656 10.800781 86.589844 10.800781 92.839844 C 10.800781 99.089844 13.28125 105.082031 17.703125 109.503906 C 22.121094 113.921875 28.113281 116.40625 34.363281 116.40625 C 40.613281 116.40625 46.605469 113.921875 51.027344 109.503906 C 55.445313 105.082031 57.925781 99.089844 57.925781 92.839844 Z M 57.925781 92.839844 "/>
|
||||||
|
</g>
|
||||||
|
</svg>
|
||||||
|
After Width: | Height: | Size: 11 KiB |
30
assets/p4-explain.svg
Normal file
30
assets/p4-explain.svg
Normal file
@ -0,0 +1,30 @@
|
|||||||
|
<?xml version="1.0" encoding="UTF-8"?>
|
||||||
|
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" width="540pt" height="413pt" viewBox="0 0 540 413" version="1.1">
|
||||||
|
<defs>
|
||||||
|
<clipPath id="clip1">
|
||||||
|
<path d="M 472 345 L 540 345 L 540 412.320313 L 472 412.320313 Z M 472 345 "/>
|
||||||
|
</clipPath>
|
||||||
|
</defs>
|
||||||
|
<g id="surface6">
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 49.179688 213.152344 L 282.046875 298.332031 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 49.171875 199.527344 L 281.894531 114.035156 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 312.601563 289.367188 L 497.34375 45.925781 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 319.199219 311.992188 L 490.84375 375.4375 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 319.042969 100.359375 L 490.742188 37.011719 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 312.445313 122.972656 L 497.4375 366.539063 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 282.046875 298.332031 Z M 282.046875 298.332031 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 281.894531 114.035156 Z M 281.894531 114.035156 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 497.34375 45.925781 Z M 497.34375 45.925781 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 490.84375 375.4375 Z M 490.84375 375.4375 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 490.742188 37.011719 Z M 490.742188 37.011719 "/>
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 497.4375 366.539063 Z M 497.4375 366.539063 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 50.382813 206.351563 C 50.382813 201.105469 48.300781 196.070313 44.585938 192.359375 C 40.875 188.648438 35.839844 186.5625 30.59375 186.5625 C 25.34375 186.5625 20.308594 188.648438 16.597656 192.359375 C 12.886719 196.070313 10.800781 201.105469 10.800781 206.351563 C 10.800781 211.601563 12.886719 216.636719 16.597656 220.347656 C 20.308594 224.058594 25.34375 226.144531 30.59375 226.144531 C 35.839844 226.144531 40.875 224.058594 44.585938 220.347656 C 48.300781 216.636719 50.382813 211.601563 50.382813 206.351563 Z M 50.382813 206.351563 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 320.429688 305.132813 C 320.429688 299.882813 318.34375 294.847656 314.628906 291.136719 C 310.917969 287.425781 305.886719 285.339844 300.636719 285.339844 C 295.386719 285.339844 290.351563 287.425781 286.640625 291.136719 C 282.929688 294.847656 280.84375 299.882813 280.84375 305.132813 C 280.84375 310.382813 282.929688 315.414063 286.640625 319.128906 C 290.351563 322.839844 295.386719 324.925781 300.636719 324.925781 C 305.886719 324.925781 310.917969 322.839844 314.628906 319.128906 C 318.34375 315.414063 320.429688 310.382813 320.429688 305.132813 Z M 320.429688 305.132813 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 320.265625 107.210938 C 320.265625 101.960938 318.179688 96.925781 314.46875 93.214844 C 310.757813 89.503906 305.722656 87.417969 300.476563 87.417969 C 295.226563 87.417969 290.191406 89.503906 286.480469 93.214844 C 282.769531 96.925781 280.683594 101.960938 280.683594 107.210938 C 280.683594 112.460938 282.769531 117.492188 286.480469 121.207031 C 290.191406 124.917969 295.226563 127.003906 300.476563 127.003906 C 305.722656 127.003906 310.757813 124.917969 314.46875 121.207031 C 318.179688 117.492188 320.265625 112.460938 320.265625 107.210938 Z M 320.265625 107.210938 "/>
|
||||||
|
<path style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 529.101563 30.160156 C 529.101563 24.910156 527.015625 19.875 523.304688 16.164063 C 519.59375 12.453125 514.558594 10.367188 509.308594 10.367188 C 504.058594 10.367188 499.027344 12.453125 495.316406 16.164063 C 491.601563 19.875 489.515625 24.910156 489.515625 30.160156 C 489.515625 35.410156 491.601563 40.445313 495.316406 44.15625 C 499.027344 47.867188 504.058594 49.953125 509.308594 49.953125 C 514.558594 49.953125 519.59375 47.867188 523.304688 44.15625 C 527.015625 40.445313 529.101563 35.410156 529.101563 30.160156 Z M 529.101563 30.160156 "/>
|
||||||
|
<path style=" stroke:none;fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;" d="M 529.199219 382.300781 C 529.199219 377.050781 527.113281 372.019531 523.402344 368.304688 C 519.691406 364.59375 514.65625 362.507813 509.40625 362.507813 C 504.160156 362.507813 499.125 364.59375 495.414063 368.304688 C 491.699219 372.019531 489.617188 377.050781 489.617188 382.300781 C 489.617188 387.550781 491.699219 392.585938 495.414063 396.296875 C 499.125 400.007813 504.160156 402.09375 509.40625 402.09375 C 514.65625 402.09375 519.691406 400.007813 523.402344 396.296875 C 527.113281 392.585938 529.199219 387.550781 529.199219 382.300781 Z M 529.199219 382.300781 "/>
|
||||||
|
<g clip-path="url(#clip1)" clip-rule="nonzero">
|
||||||
|
<path style="fill:none;stroke-width:3.78;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:3.25;" d="M 529.199219 382.300781 C 529.199219 377.050781 527.113281 372.019531 523.402344 368.304688 C 519.691406 364.59375 514.65625 362.507813 509.40625 362.507813 C 504.160156 362.507813 499.125 364.59375 495.414063 368.304688 C 491.699219 372.019531 489.617188 377.050781 489.617188 382.300781 C 489.617188 387.550781 491.699219 392.585938 495.414063 396.296875 C 499.125 400.007813 504.160156 402.09375 509.40625 402.09375 C 514.65625 402.09375 519.691406 400.007813 523.402344 396.296875 C 527.113281 392.585938 529.199219 387.550781 529.199219 382.300781 Z M 529.199219 382.300781 "/>
|
||||||
|
</g>
|
||||||
|
</g>
|
||||||
|
</svg>
|
||||||
|
After Width: | Height: | Size: 6.7 KiB |
12
assets/p5-explain-bad.svg
Normal file
12
assets/p5-explain-bad.svg
Normal file
@ -0,0 +1,12 @@
|
|||||||
|
<?xml version="1.0" encoding="UTF-8"?>
|
||||||
|
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 2.04 2.04" version="1.1">
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.27" cy="1.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.27" cy="0.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.27" cy="0.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.27" cy="0.77" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.77" cy="1.77" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.77" cy="1.27" r="0.1"/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 0.354971 1.22751 L 1.18503 0.812485 "/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 0.300042 0.360125 L 0.739958 1.67988 "/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 1.31249 0.354971 L 1.72751 1.18503 "/>
|
||||||
|
</svg>
|
||||||
|
After Width: | Height: | Size: 1.8 KiB |
21
assets/p5-explain-bad.txt
Normal file
21
assets/p5-explain-bad.txt
Normal file
@ -0,0 +1,21 @@
|
|||||||
|
OutputFile="p5-explain-ok.svg"
|
||||||
|
R=.1
|
||||||
|
Thickness=.01
|
||||||
|
BorderColor="#616161"
|
||||||
|
ColorMap:r="#FF7043"
|
||||||
|
ColorMap:b="#29B6F6"
|
||||||
|
Xaxis="right"
|
||||||
|
Yaxis="Down"
|
||||||
|
---
|
||||||
|
6
|
||||||
|
1 -1 b
|
||||||
|
2 -2 b
|
||||||
|
1 -2 b
|
||||||
|
2 -1.5 r
|
||||||
|
1.5 -.5 r
|
||||||
|
2.5 -1 r
|
||||||
|
|
||||||
|
3
|
||||||
|
1 4
|
||||||
|
3 5
|
||||||
|
2 6
|
||||||
12
assets/p5-explain-ok.svg
Normal file
12
assets/p5-explain-ok.svg
Normal file
@ -0,0 +1,12 @@
|
|||||||
|
<?xml version="1.0" encoding="UTF-8"?>
|
||||||
|
<svg xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" viewBox="0 0 2.04 2.04" version="1.1">
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.27" cy="1.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.27" cy="0.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#29B6F6;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.27" cy="0.27" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.27" cy="0.77" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="0.77" cy="1.77" r="0.1"/>
|
||||||
|
<circle style="fill-rule:evenodd;fill:#FF7043;fill-opacity:1;stroke-width:0.01;stroke-linecap:square;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" cx="1.77" cy="1.27" r="0.1"/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 0.354971 0.312485 L 1.18503 0.727515 "/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 1.31249 0.354971 L 1.72751 1.18503 "/>
|
||||||
|
<path style="fill:none;stroke-width:0.01;stroke-linecap:butt;stroke-linejoin:miter;stroke:#616161;stroke-miterlimit:0.007;" d="M 0.337175 1.33718 L 0.702825 1.70282 "/>
|
||||||
|
</svg>
|
||||||
|
After Width: | Height: | Size: 1.8 KiB |
21
assets/p5-explain-ok.txt
Normal file
21
assets/p5-explain-ok.txt
Normal file
@ -0,0 +1,21 @@
|
|||||||
|
OutputFile="p5-explain-ok.svg"
|
||||||
|
R=.1
|
||||||
|
Thickness=.01
|
||||||
|
BorderColor="#616161"
|
||||||
|
ColorMap:r="#FF7043"
|
||||||
|
ColorMap:b="#29B6F6"
|
||||||
|
Xaxis="right"
|
||||||
|
Yaxis="Down"
|
||||||
|
---
|
||||||
|
6
|
||||||
|
1 -1 b
|
||||||
|
2 -2 b
|
||||||
|
1 -2 b
|
||||||
|
2 -1.5 r
|
||||||
|
1.5 -.5 r
|
||||||
|
2.5 -1 r
|
||||||
|
|
||||||
|
3
|
||||||
|
3 4
|
||||||
|
2 6
|
||||||
|
1 5
|
||||||
44
lib.typ
Normal file
44
lib.typ
Normal file
@ -0,0 +1,44 @@
|
|||||||
|
#import "template.typ": *
|
||||||
|
|
||||||
|
#let pagebreak_until_odd() = locate(loc => {
|
||||||
|
pagebreak()
|
||||||
|
locate(loc => if calc.even(thispage_number(loc)) {
|
||||||
|
skip_footer.update(true)
|
||||||
|
pagebreak()
|
||||||
|
skip_footer.update(false)
|
||||||
|
})
|
||||||
|
})
|
||||||
|
|
||||||
|
#let italic(body) = text(style: "italic", body)
|
||||||
|
|
||||||
|
#let type_icon(name, color) = square(size: 45pt, fill: rgb(color))[
|
||||||
|
#set text(22pt, white, font: "Arial", weight: "regular")
|
||||||
|
#set align(center + horizon)
|
||||||
|
#name
|
||||||
|
]
|
||||||
|
|
||||||
|
#let combinatorics_icon = type_icon("C", "FBC02D")
|
||||||
|
#let algebra_icon = type_icon("Al", "EC407A")
|
||||||
|
#let analysis_icon = type_icon("An", "FFA000")
|
||||||
|
#let number_thoery_icon = type_icon("N", "2E7D32")
|
||||||
|
#let logic_icon = type_icon("L", "000000")
|
||||||
|
#let geometry_icon = type_icon("G", "283593")
|
||||||
|
|
||||||
|
#let bf(x) = {$upright(bold(#x))$}
|
||||||
|
|
||||||
|
#let hypergeometric-func(ax, bx, x) = {$upright(F)lr((mat(delim: #none, ax;bx)#h(5pt)#line(angle: 90deg, length: 40pt)#h(5pt)#x))$}
|
||||||
|
|
||||||
|
#let transpose = {$upright(sans(T))$}
|
||||||
|
|
||||||
|
#let frange = {$op("range")$}
|
||||||
|
#let dimrange = {$op("dim range")$}
|
||||||
|
|
||||||
|
#let theme_blue = rgb("29B6F6")
|
||||||
|
#let theme_red = rgb("FF7043")
|
||||||
|
#let theme_border = rgb("616161")
|
||||||
|
#let theme_black = rgb("212121")
|
||||||
|
|
||||||
|
#let math_numbering(body) = {
|
||||||
|
set math.equation(numbering: "(1)")
|
||||||
|
body
|
||||||
|
}
|
||||||
525
main.typ
Normal file
525
main.typ
Normal file
@ -0,0 +1,525 @@
|
|||||||
|
#import "template.typ": *
|
||||||
|
#import "lib.typ": *
|
||||||
|
|
||||||
|
#show: project.with(
|
||||||
|
title: "杂题选讲",
|
||||||
|
)
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
|
||||||
|
#align(center,
|
||||||
|
table(
|
||||||
|
columns: 6,
|
||||||
|
stroke: none,
|
||||||
|
..for (name, fig) in (
|
||||||
|
"组合": combinatorics_icon,
|
||||||
|
"代数": algebra_icon,
|
||||||
|
"分析": analysis_icon,
|
||||||
|
"数论": number_thoery_icon,
|
||||||
|
"几何": geometry_icon,
|
||||||
|
"数理逻辑": logic_icon
|
||||||
|
) {
|
||||||
|
(stack(dir:ttb, fig, box[
|
||||||
|
#set text(10pt)
|
||||||
|
#name
|
||||||
|
], spacing: 4pt),)
|
||||||
|
}
|
||||||
|
)
|
||||||
|
)
|
||||||
|
|
||||||
|
#let problem_type = state("problem_type", ())
|
||||||
|
|
||||||
|
#show heading.where(level: 1): it => {
|
||||||
|
problem_id.step()
|
||||||
|
footer_title.update(it.body)
|
||||||
|
block(width: 100%)[
|
||||||
|
#place(
|
||||||
|
right + top,
|
||||||
|
dx: -5pt,
|
||||||
|
dy: -5pt,
|
||||||
|
stack(
|
||||||
|
dir: ltr,
|
||||||
|
spacing: 4pt,
|
||||||
|
..for t in problem_type.at(it.location()) {
|
||||||
|
(t,)
|
||||||
|
}
|
||||||
|
)
|
||||||
|
)
|
||||||
|
#set text(weight: "light", font: cnfont)
|
||||||
|
#block[
|
||||||
|
#set text(2em)
|
||||||
|
\##problem_id.display("1")
|
||||||
|
]
|
||||||
|
#block(fill: rgb("B3E5FC"))[
|
||||||
|
#set text(1.5em)
|
||||||
|
#h(.3em)
|
||||||
|
#it.body
|
||||||
|
]
|
||||||
|
#v(25pt)
|
||||||
|
]}
|
||||||
|
|
||||||
|
<MainStarted>
|
||||||
|
|
||||||
|
#pagebreak_until_odd()
|
||||||
|
#problem_type.update((combinatorics_icon,))
|
||||||
|
= 随机游走的左端点
|
||||||
|
|
||||||
|
一个长度为 $n$ 的由 $-1$ 或 1 构成的序列 $a$,其中 1 的个数为 $c$ 个。我们称一个子区间合法是指该子区间的数的和大于等于 0。求证:所有合法子区间的左端点的数量不超过 $2c$ 个。
|
||||||
|
|
||||||
|
== 提示
|
||||||
|
|
||||||
|
子区间是指序列中连续的一段,形式化地说,问题是求证:
|
||||||
|
|
||||||
|
$ abs(lr({l in NN[1..n] : exists l in NN[l..n],(sum_(k=l)^r a_k)>=0}))<=2c $
|
||||||
|
|
||||||
|
举个例子,若 $n=8,c=3$,序列 $a$ 为
|
||||||
|
|
||||||
|
$ -1,1,1,-1,-1,1,-1,-1 $
|
||||||
|
|
||||||
|
那么序列 $a$ 中所有合法子区间的左端点共有 5 个,为下面括号的位置
|
||||||
|
|
||||||
|
$ (-1),(1),(1),-1,(-1),(1),-1,-1 $
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
|
||||||
|
== 解答
|
||||||
|
|
||||||
|
对于某个序列 $a$,记 $S(a)$ 表示序列 $a$ 中所有合法子区间的左端点的数量。
|
||||||
|
|
||||||
|
如果 $a$ 存在一个 $-1$ 在一个 1 的后面,即存在下标 $i,j$ 满足 $i<j$ 且 $a_i=1,a_j=-1$,那么交换 $i,j$ 位置上的值后,得到一个新序列 $a'$,显然 $a'$ 中 1 的数量也为 $c$。
|
||||||
|
|
||||||
|
*引理* 进行上述变换后所有合法子区间的左端点的数量不降,即 $S(a)<= S(a')$ 一定成立。
|
||||||
|
|
||||||
|
假设上述引理成立,那么我们就只需要论证由 $n-c$ 个 $-1$ 开头,然后 $c$ 个 1 组成的序列 $b$ 满足 $S(b)<= 2c$,这是显然的。而对于任何其他序列,它们都可以通过有限次上述变换得到序列 $b$。
|
||||||
|
|
||||||
|
下面我们证明该引理成立,考虑序列 $a$ 的前缀和序列 $p$,
|
||||||
|
|
||||||
|
$ p_k=sum_(i=1)^k a_i $
|
||||||
|
|
||||||
|
那么左开右闭区间 $(l..r]$ 合法等价于 $p_r-p_l>=0$。设我们要交换序列 $a$ 中的 $i,j$ 位置,由于 $a_i=1$,所以 $p_(i-1)=p_i-1$ 。若某个位置 $k<i$ 本来某个合法区间的左端点,而交换 $i,j$ 位置上的值后它就不是了,那么一定有 $p_k=p_i$。
|
||||||
|
|
||||||
|
那么找出 $i$ 前面第一个 $p_k=p_i$ 的位置(如果有)后,$k$ 以前的左端点都不会改变,因为 $p_k=p_i$ 说明 $i,k$ 位置是等价的。这说明 $S(a)<= S(a')$。
|
||||||
|
|
||||||
|
#pagebreak_until_odd()
|
||||||
|
#problem_type.update((combinatorics_icon,))
|
||||||
|
= 取完全部球的时间
|
||||||
|
|
||||||
|
有 $n m$ 个彩色小球,其中有 $n$ 种不同颜色,每种颜色各 $m$ 个球。现在每次均匀地随机取出一个小球(取出之后不放回去),则期望上取出多少个球后可以取完某种颜色的球?
|
||||||
|
|
||||||
|
== 提示
|
||||||
|
|
||||||
|
容易发现相同颜色的球是否视为一样对答案没有影响。
|
||||||
|
|
||||||
|
在这个问题中,当有 2 种颜色,每种颜色有 3 个球时(即 $n=2,m=3$),符合题目要求的取球方案共 20 种,枚举如下:
|
||||||
|
|
||||||
|
#let colored_circle_stack(colors, size: 10pt, numbered: false, active_number: none) = box(
|
||||||
|
width: if numbered { (size * 2.5) * colors.len() - size / 2 } else {size * (1 + colors.len())},
|
||||||
|
height: size * 2,
|
||||||
|
for i in range(colors.len()) {
|
||||||
|
place(
|
||||||
|
left + top,
|
||||||
|
dx: if numbered { 2.5 * i * size } else { i * size },
|
||||||
|
circle(
|
||||||
|
radius: size,
|
||||||
|
stroke: if i + 1 == active_number {
|
||||||
|
2pt + theme_black
|
||||||
|
} else {
|
||||||
|
1pt + theme_border
|
||||||
|
},
|
||||||
|
fill: if colors.at(i) == "r" {
|
||||||
|
theme_red
|
||||||
|
} else if colors.at(i) == "b" {
|
||||||
|
theme_blue
|
||||||
|
} else {
|
||||||
|
black
|
||||||
|
},
|
||||||
|
if numbered {
|
||||||
|
[
|
||||||
|
#set align(center + horizon)
|
||||||
|
#set text(font: cnfont, white)
|
||||||
|
#(i + 1)
|
||||||
|
]
|
||||||
|
}
|
||||||
|
)
|
||||||
|
)
|
||||||
|
}
|
||||||
|
)
|
||||||
|
|
||||||
|
#figure(
|
||||||
|
table(
|
||||||
|
columns: 2,
|
||||||
|
align: center + horizon,
|
||||||
|
[3], {
|
||||||
|
colored_circle_stack("rrrbbb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("bbbrrr")
|
||||||
|
},
|
||||||
|
[4], {
|
||||||
|
colored_circle_stack("rrbrbb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rbrrbb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rbbbrr")
|
||||||
|
linebreak()
|
||||||
|
colored_circle_stack("brrrbb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("brbbrr")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("bbrbrr")
|
||||||
|
},
|
||||||
|
[5], {
|
||||||
|
colored_circle_stack("rrbbrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rrbbbr")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rbrbrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rbrbbr")
|
||||||
|
linebreak()
|
||||||
|
colored_circle_stack("rbbrrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("rbbrbr")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("brrbrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("brrbbr")
|
||||||
|
linebreak()
|
||||||
|
colored_circle_stack("brbrrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("brbrbr")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("bbrrrb")
|
||||||
|
h(10pt)
|
||||||
|
colored_circle_stack("bbrrbr")
|
||||||
|
}
|
||||||
|
),
|
||||||
|
caption: [枚举 2 种颜色,每种 3 个球时所有可能的 20 种情况]
|
||||||
|
)
|
||||||
|
|
||||||
|
容易看出,其中取出 3 个球后可以取完某种颜色的球的方案 2 种,取出 4 个球的方案 6 种,取出 5 个球的方案 12 种,故 $n=2,m=3$ 时的答案为
|
||||||
|
|
||||||
|
$ 2/20 times 3+6/20 times 4+12/20 times 5=9/2 $
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
== 解答
|
||||||
|
|
||||||
|
我们用记号 $bf(E)(a)$ 表示随机试验中变量 $a$ 的数学期望。已经取出的球的数量简称为时刻,例如“取出某种颜色全部球的时刻”的意思是“取出某种颜色全部球时已经取出的球的数量”。
|
||||||
|
|
||||||
|
我们考虑给同种颜色的球编上 1 到 $n$ 的编号,这样这 $n m$ 个球各不相同,显然是否编号这对答案没有影响。按某种顺序取出这 $n m$ 个球全部取出,有 $(n m)!$ 种取法。
|
||||||
|
|
||||||
|
考虑把取球序列翻转过来,则原问题可以转化为 *第一次取出每种颜色的球至少一个的时刻*。举个例子,若 $n=2,m=3$,考虑下面取出球的序列:
|
||||||
|
|
||||||
|
#figure(colored_circle_stack("rbrrbb", numbered: true, active_number: 4))
|
||||||
|
|
||||||
|
如图,在第 4 次操作后(图中加粗位置),红色的球被全部取出了,此时把取球序列翻转就得到:
|
||||||
|
|
||||||
|
#figure(colored_circle_stack("bbrrbr", numbered: true, active_number: 3))
|
||||||
|
|
||||||
|
如图,在第 3 次操作后,全部颜色的球都被取出了至少一次,注意到这里的第 3 个球就是反转前的第 4 个球(由于翻转位置发生了改变,具体而言位置 $p$ 会变到位置 $n m+1-p$)。
|
||||||
|
|
||||||
|
设 $S$ 表示每种颜色首次出现的时刻的可重集合,现在就是要求 $bf(E)(max S)$ 的值。根据容斥原理(min-max容斥),有
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
$ bf(E)(max S)=sum_(T subset.eq S,T eq.not nothing)(-1)^(abs(T)-1)bf(E)(min T) $ <P2EqEmaxS1>
|
||||||
|
]
|
||||||
|
|
||||||
|
考虑 $bf(E)(min T)$ 的组合意义,可以看出它表示“首次出现 $T$ 集合中的任意一种颜色的球的时刻”,枚举这个时刻,得到
|
||||||
|
|
||||||
|
$ bf(E)(min T)=sum_(t\geq 0)(binom((n-abs(T))m,t)t!)/(binom(n m,t)t!)(t+1)(abs(T)m)/(n m-t) $
|
||||||
|
|
||||||
|
注意到这个式子只与集合 $T$ 的大小有关,而与 $T$ 中具体包含那些元素无关,因此考虑记
|
||||||
|
|
||||||
|
$ f(k)=sum_(t\geq 0)(binom((n-k)m,t)t!)/(binom(n m,t)t!)(t+1)(k m)/(n m-t) $
|
||||||
|
|
||||||
|
于是 $ bf(E)(min T)=f(abs(T)) $,代入@P2EqEmaxS1 得到,
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
$ bf(E)(max S)=sum_(T subset.eq S,T eq.not nothing)(-1)^(abs(T)-1) f(abs(T)) $ <P2EqEmaxS2>
|
||||||
|
]
|
||||||
|
|
||||||
|
我们首先专注于解出 $f(k)$ 的简化形式,展开二项式系数并通分,得到 $f(k)=sum_(t>=0)w_t$,其中
|
||||||
|
|
||||||
|
$ w_t=(((n-k)m)!(n m-t)!)/(((n-k)m-t)!(n m)!)(t+1)(k m)/(n m-t) $
|
||||||
|
|
||||||
|
,其相邻两项的比值由
|
||||||
|
|
||||||
|
$ (w_(t+1))/(w_t)&=((t+2) (m n-t) (m n-t-1)! (m (n-k)-t)!)/((t+1) (m n-t-1) (m n-t)! (m (n-k)-t-1)!)
|
||||||
|
\ &=((t+2)(t+k m-n m))/((t+1-n m)(t+1)) $
|
||||||
|
|
||||||
|
给出,这个比值可以看成关于 $t$ 的有理函数,因此可以将原式写作超几何函数的形式:
|
||||||
|
|
||||||
|
$ f(k)=k/n #hypergeometric-func($2, k m - n m$, $1 - n m$, 1) $
|
||||||
|
|
||||||
|
由组合意义可知,一定有 $k m-n m>=0$,因此可以应用范德蒙德卷积恒等式对其进行化简:
|
||||||
|
|
||||||
|
$ f(k)&=k/n (Gamma(- 1 - k m)Gamma(1 - n m))/(Gamma(- 1 - n m)Gamma(1 - k m))
|
||||||
|
\ &= (n m+1)/(k m+1) $
|
||||||
|
|
||||||
|
把这个化简后的结果代回@P2EqEmaxS2,然后再次转化为超几何函数并使用德蒙德卷积恒等式化简,可以解出
|
||||||
|
|
||||||
|
|
||||||
|
$ bf(E)(max S)&=sum_(T subset.eq S,T eq.not nothing) (-1)^(abs(T)-1) (n m+1)/(abs(T)m+1)
|
||||||
|
\ &= sum_(k=1)^n (-1)^(k-1) binom(n,k)(n m+1)/(k m+1)
|
||||||
|
\ &= (1 + n m) - (1 + n m) #hypergeometric-func($1 + k m, k - n$, $1 + m + k m$, 1)
|
||||||
|
\ &= n m + 1 - ((1 / m - 1)!n!)/((n+1/m - 1)!) $
|
||||||
|
|
||||||
|
|
||||||
|
注意,这个式子给出的是翻转过后的期望时刻,转化为原来问题才能得到最终答案:
|
||||||
|
|
||||||
|
$ bf(E)=((1 / m - 1)!n!)/((n+1/m - 1)!) $
|
||||||
|
|
||||||
|
#pagebreak_until_odd()
|
||||||
|
#problem_type.update((algebra_icon,))
|
||||||
|
= 社团数量的上限
|
||||||
|
|
||||||
|
现在有 $n$ 个人要成立若干个社团(一个人可以属于多个社团)满足:
|
||||||
|
|
||||||
|
- 每个社团的人数均为奇数;
|
||||||
|
- 任意两个不同的社团所共有的成员数量为偶数。
|
||||||
|
|
||||||
|
求证:所能成立的社团数量不超过 $n$ 个。
|
||||||
|
|
||||||
|
== 提示
|
||||||
|
|
||||||
|
形式化地说,记 $U={1,2,dots,n}$,已知集簇 $S subset.eq 2^U$ 满足对于任意 $A,B in S$,$abs(A sect B)$ 为奇数当且仅当 $A=B$。求证 $abs(S)<= n$。
|
||||||
|
|
||||||
|
容易发现,只要每个人均成立一个只包含自己的社团,就可以成立恰好 $n$ 个社团,满足每个社团的人数均为奇数(1 个),任意两个不同的社团所共有的成员数量为偶数(0 个)。
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
== 解答
|
||||||
|
|
||||||
|
|
||||||
|
假设已经确定了某种成立 $m$ 个社团的方案,第 $i(1<= i<= m)$ 个社团包含的成员的集合记作 $C_i$。
|
||||||
|
|
||||||
|
|
||||||
|
我们考虑一个二元域 $bb(Z)_2$,包含 ${0,1}$ 两个元素,在域上定义模 2 意义下的加法和乘法:
|
||||||
|
|
||||||
|
#[
|
||||||
|
#let cell_size = 30pt
|
||||||
|
#figure(stack(
|
||||||
|
dir: ltr,
|
||||||
|
spacing: cell_size,
|
||||||
|
table(
|
||||||
|
align: center + horizon,
|
||||||
|
columns: (cell_size, cell_size, cell_size),
|
||||||
|
rows: (cell_size, cell_size, cell_size),
|
||||||
|
$ + $, $ 0 $, $ 1 $,
|
||||||
|
$ 0 $, $ 0 $, $ 1 $,
|
||||||
|
$ 1 $, $ 1 $, $ 0 $,
|
||||||
|
),
|
||||||
|
table(
|
||||||
|
align: center + horizon,
|
||||||
|
columns: (cell_size, cell_size, cell_size),
|
||||||
|
rows: (cell_size, cell_size, cell_size),
|
||||||
|
$ times $, $ 0 $, $ 1 $,
|
||||||
|
$ 0 $, $ 0 $, $ 0 $,
|
||||||
|
$ 1 $, $ 0 $, $ 1 $,
|
||||||
|
)
|
||||||
|
), caption: [ $bb(Z)_2$ 上的加法和乘法 ])
|
||||||
|
]
|
||||||
|
|
||||||
|
构造 $ bb(Z)_2^(m times n)$ 上的矩阵 $A$,满足
|
||||||
|
|
||||||
|
$ A_(i,j)=cases(1 quad& j in C_i
|
||||||
|
\ 0 & j in.not C_i) $
|
||||||
|
|
||||||
|
考虑 $A A^transpose$ 这两个矩阵的乘积,是一个 $m times m$ 的矩阵,根据其第 $i$ 行第 $j$ 列的值所代表的实际意义,容易看出
|
||||||
|
|
||||||
|
|
||||||
|
$ (A A^transpose)_(i,j)=cases(1 quad& abs(C_i sect C_j) mtext("是奇数")
|
||||||
|
\ 0 & abs(C_i sect C_j) mtext("是偶数")) $
|
||||||
|
|
||||||
|
|
||||||
|
根据题目的约束条件,$abs(C_i sect C_j)$ 是奇数当且仅当 $i=j$,所以对角线上的数均为 1,其余位置的数均为 0,于是
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
$ A A^transpose= bf(I)_m $ <P2eq1>
|
||||||
|
|
||||||
|
其中 $bf(I)_m$ 表示 $m$ 阶单位矩阵。
|
||||||
|
|
||||||
|
我们用 $dim V$ 表示线性空间 $V$ 的维数,$frange T$ 表示线性变换 $T$ 的值域。由于 $A$ 是 $bb(Z)_2^n->bb(Z)_2^m$ 的线性变换,其值域的维数一定满足@P2inq1[不等式]。由于 $bf(I)_m$ 是 $bb(Z)_2^m->bb(Z)_2^m$ 的线性变换,其值域的维数一定满足@P2inq2[等式]。
|
||||||
|
|
||||||
|
|
||||||
|
$ dimrange A<= n $ <P2inq1>
|
||||||
|
|
||||||
|
$ dimrange bf(I)_m=m $ <P2inq2>
|
||||||
|
|
||||||
|
|
||||||
|
另一方面,因为 $frange A A^transpose subset.eq frange A$,所以
|
||||||
|
|
||||||
|
|
||||||
|
#show: math_numbering
|
||||||
|
$ dimrange A A^transpose<=dimrange A $ <P2inq3>
|
||||||
|
]
|
||||||
|
|
||||||
|
联立上面的@P2eq1、@P2inq1、@P2inq2、@P2inq3,就立即给出了我们欲证的结果:
|
||||||
|
|
||||||
|
$ m=dimrange bf(I)=dimrange A A^transpose<=dimrange A<=n $
|
||||||
|
|
||||||
|
这表明 $m<= n$ 始终成立,原命题得证。
|
||||||
|
|
||||||
|
#pagebreak_until_odd()
|
||||||
|
#problem_type.update((combinatorics_icon,analysis_icon,))
|
||||||
|
= 不含三元环的最大边数
|
||||||
|
|
||||||
|
已知无向图 $G$ 由 $n$ 个点组成,且不包含三元环,求 $G$ 边数的最大值。
|
||||||
|
|
||||||
|
== 提示
|
||||||
|
|
||||||
|
设 $G=(V,E)$ 是一个无向图。我们称图 $G$ 中的一个“三元环”是指图 $G$ 中的三个点 $a,b,c$,满足 ${(a,b),(b,c),(a,c)} subset.eq E$。
|
||||||
|
|
||||||
|
例如当 $n=5$ 时,下面是一个不包含三元环的图的例子:
|
||||||
|
|
||||||
|
#figure(image(
|
||||||
|
"./assets/p4-explain.svg",
|
||||||
|
width: 80%
|
||||||
|
), caption: [一个没有三元环的示例图])
|
||||||
|
|
||||||
|
该图包含 5 个点和 6 条边,可以证明所有没有三元环的由 5 个点构成的无向图的边均不超过 6 条。
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
== 解答
|
||||||
|
|
||||||
|
对于这种求最大值的问题,我们一般首先尝试给出一种可行的构造,再证明它是最优的。
|
||||||
|
|
||||||
|
把图中的 $n$ 个点分为 2 个大小尽可能的集合 $A$ 和 $B$(即大小分别为 $floor(n/2)$ 和 $ceil(n/2)$),然后对于每对点 $a in A,b in B$,在点 $a$ 和点 $b$ 之间连一条边,并且不连接其他的任何边。这样得到的图中一共连接了 $floor(n^2/4)$ 条边,且由于任意两个属于同一个集合的点之间都没有连边,这个图中不包含任何三元环。这样的图被称为“完全二分图”。
|
||||||
|
|
||||||
|
#figure(image(
|
||||||
|
"./assets/p4-bipart.svg",
|
||||||
|
width: 60%
|
||||||
|
), caption: [7 个点的完全二分图,包含 12 条边])
|
||||||
|
|
||||||
|
下面我们要证明这个构造是最优的构造,即任何由 $n$ 个点组成,不包含三元环的无向图的边数都不可能超过 $floor(n^2/4)$。这里将给出 3 种不同的证明。
|
||||||
|
|
||||||
|
=== 证明 A
|
||||||
|
|
||||||
|
#[
|
||||||
|
|
||||||
|
#let dd = {$upright(d)$}
|
||||||
|
|
||||||
|
设 $G=(V,E)$ 是某个无向图,包含 $n$ 个点 $m$ 条边。点 $v$ 的度数是指连接点 $v$ 的边的数量,记作 $dd(v)$。于是有
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
|
||||||
|
$ sum_(x in V)dd(x)=2m $ <P4prove1eq1>
|
||||||
|
|
||||||
|
$ sum_(x in V)dd^2(x)=sum_((x,y)in E)dd(x)+dd(y) $ <P4prove1eq2>
|
||||||
|
]
|
||||||
|
|
||||||
|
现在假设 $G$ 不包含三元环。若 $(x,y)$ 是图 $G$ 的边,那么对于任意一个点 $v$,一定有 $(x,v)in.not E$ 或 $(y,v)in.not E$,这说明
|
||||||
|
|
||||||
|
$ dd(x)+dd(y)<= n $
|
||||||
|
|
||||||
|
将这个性质代入@P4prove1eq2,得到
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
|
||||||
|
$ sum_((x,y)in E)dd(x)+dd(y)<= n m $ <P4prove1eq3>
|
||||||
|
|
||||||
|
另一方面,对@P4prove1eq1 使用柯西-施瓦茨不等式得到
|
||||||
|
|
||||||
|
$ sum_(x in V)dd^2(x)>=1/n lr((sum_(x in V)dd(x)))^2=(4m^2)/n $ <P4prove1eq4>
|
||||||
|
]
|
||||||
|
|
||||||
|
联立@P4prove1eq2、@P4prove1eq3、@P4prove1eq4,得到
|
||||||
|
|
||||||
|
$ (4m^2)/n<=sum_(x in V)dd^2(x)=sum_((x,y)in E)dd(x)+dd(y)<=n m $
|
||||||
|
|
||||||
|
整理得到 $m<= n^2slash 4$,注意到 $n$ 为整数,于是 $m<=floor(n^2slash 4)$,命题得证。
|
||||||
|
|
||||||
|
=== 证明 B
|
||||||
|
|
||||||
|
设 $G=(V,E)$ 是某个不包含三元环的无向图,包含 $n$ 个点 $m$ 条边。两个点 $a,b in V$ 之间有连边,则称这两个点是“相邻的”,与点 $a$ 相邻的所有点构成的集合记作 $N(a)$。
|
||||||
|
|
||||||
|
由于 $G$ 不包含三元环,所以对于图中的任意一个点 $a$,与 $a$ 的相邻的点构成的集合 $N(a)$ 一定是独立集,即 $N(a)$ 中的任意两个都不是相邻的。
|
||||||
|
|
||||||
|
设 $A subset.eq V$ 是图 $G$ 中的一个最大独立集,那么对于任意一个点 $x$,一定有
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
|
||||||
|
$ dd(x)<=abs(A) $ <P4prove2eq1>
|
||||||
|
]
|
||||||
|
|
||||||
|
令 $B=V without A$。由于 $A$ 是独立集,所以 $G$ 中的每条边都至少有一个端点包含在 $B$ 中。于是
|
||||||
|
|
||||||
|
$ m<=sum_(x in B)dd(x)<=sum_(x in B)abs(A)=abs(A)abs(B)<=((abs(A)+abs(B))/2)^2=(n^2)/4 $
|
||||||
|
|
||||||
|
其中第二个不等号使用了@P4prove2eq1,第三个不等号使用了均值不等式。注意到 $n$ 为整数,于是 $m<=floor(n^2slash 4)$,命题得证。
|
||||||
|
|
||||||
|
=== 证明 C
|
||||||
|
|
||||||
|
设 $G=(V,E)$ 是某个不包含三元环的无向图,包含 $n$ 个点 $m$ 条边。考虑一个随机均匀的排列顶点排列 $sigma$,令
|
||||||
|
|
||||||
|
$ X={v in V:v mtext("与") sigma mtext("中所有早于") v mtext("出现的顶点相邻")} $
|
||||||
|
|
||||||
|
由于排列是均匀随机选择的,以及一个顶点 $x in X$ 当且仅当它出现在其所有不相邻的顶点之前,我们有
|
||||||
|
|
||||||
|
#[
|
||||||
|
#show: math_numbering
|
||||||
|
|
||||||
|
$ bf(P)(v in X)=1/(n-dd(v)) $ <P4prove3eq>
|
||||||
|
]
|
||||||
|
|
||||||
|
其中 $bf(P)(e)$ 表示事件 $e$ 发生的概率。另一方面,考虑 $X$ 的组合意义,注意到 $X$ 中的顶点集合形成一个团(图 $G$ 的子图,并且是完全图),所以一定有 $abs(X)<=2$,这给出
|
||||||
|
|
||||||
|
$ 2>=bf(E)(abs(X))=sum_(v in V)bf(P)(v in X)=sum_(v in V)1/(n-dd(v))>=n/(n-2m slash n) $
|
||||||
|
|
||||||
|
其中 $bf(E)(a)$ 表示随机试验中变量 $a$ 的数学期望。第一个等号使用了数学期望的定义,第二个等号使用了@P4prove3eq,第二个不等号利用了函数的凸性,也即琴生不等式。这个式子整理得到 $m<=n^2 slash 4$,原命题得证。
|
||||||
|
|
||||||
|
这个证明使用了现代组合学中的一种名为“概率方法”的技术。在这种方法中,人们以一种巧妙的方式向确定性问题中引入随机性来得到一个确定性的结果。
|
||||||
|
|
||||||
|
]
|
||||||
|
|
||||||
|
#pagebreak_until_odd()
|
||||||
|
#problem_type.update((geometry_icon,))
|
||||||
|
= 无交点的匹配方案
|
||||||
|
|
||||||
|
平面上有红色点和蓝色点各 $n$ 个,且这 $2n$ 个点没有三个点共线。我们称一种红蓝点之间的配对方案合法,是指在每对点之间用线段连接后,得到的 $n$ 条线段没有交点。求证:一定存在一种合法的配对方案。
|
||||||
|
|
||||||
|
== 提示
|
||||||
|
|
||||||
|
形式化地说,设 $U={1,2,dots,n}$,红色点分别为 $p_1,dots,p_n$,蓝色点分别为 $q_1,dots,q_n$。一种配对方案是指 $U -> U$ 的一个双射 $f$。一种配对方案合法当且仅当线段集合 ${(p_k,q_{f(k)}):k in U}$ 中任意两条线段均不相交。
|
||||||
|
|
||||||
|
举个例子,对于红蓝各 3 个点的一种情况,下图为一种合法的配对方案,
|
||||||
|
|
||||||
|
#align(center,
|
||||||
|
stack(
|
||||||
|
dir: ltr,
|
||||||
|
figure(image(
|
||||||
|
"./assets/p5-explain-ok.svg",
|
||||||
|
width: 40%,
|
||||||
|
), caption: [一种合法方案]),
|
||||||
|
figure(image(
|
||||||
|
"./assets/p5-explain-bad.svg",
|
||||||
|
width: 40%
|
||||||
|
), caption: [一种不合法方案]),
|
||||||
|
)
|
||||||
|
)
|
||||||
|
|
||||||
|
#pagebreak()
|
||||||
|
== 解答
|
||||||
|
|
||||||
|
红蓝各 1 个点的情况的情况是平凡的,下面均假设 $n>=2$。
|
||||||
|
|
||||||
|
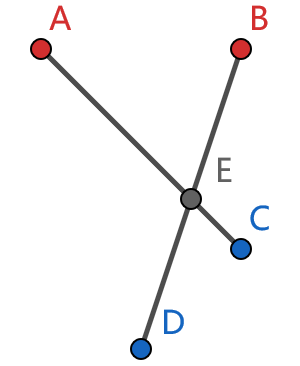
(反证法)假设不存在一种合法的配对方案。从全部配对方案中选出连接的线段长度之和最短的一种方案,根据反证假设一定存在两条线段相交,设相交的两条线段的红色端点分别为点 $A$ 和点 $B$,蓝色端点分别为点 $C$ 和点 $D$,$A$ 和 $C$ 配对,$B$ 和 $D$ 配对,$A C$ 和 $B D$ 的交点为 $E$。
|
||||||
|
|
||||||
|
/*
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
根据三角形不等式,一定有
|
||||||
|
|
||||||
|
$$\begin{aligned}|AD|&\leq|AE|+|DE|\\|BC|&\leq|BE|+|EC|\end{aligned}$$
|
||||||
|
|
||||||
|
由于没有三点共线,等号一定不成立,这说明
|
||||||
|
|
||||||
|
$$|AD|+|BC|<|AC|+|BD|$$
|
||||||
|
|
||||||
|
那么 $A$ 和 $D$、$B$ 和 $C$ 配对的方案一定比这种方案线段长度之和更短,矛盾,故假设不成立。于是合法方案一定存在。
|
||||||
|
*/
|
||||||
96
scripts/g2s.cpp
Normal file
96
scripts/g2s.cpp
Normal file
@ -0,0 +1,96 @@
|
|||||||
|
#include<bits/stdc++.h>
|
||||||
|
|
||||||
|
#define N 100
|
||||||
|
|
||||||
|
using namespace std;
|
||||||
|
|
||||||
|
struct vec
|
||||||
|
{
|
||||||
|
float x,y;
|
||||||
|
void operator += (const vec &a) {x+=a.x,y+=a.y;}
|
||||||
|
void operator -= (const vec &a) {x-=a.x,y-=a.y;}
|
||||||
|
void operator *= (float a) {x*=a,y*=a;}
|
||||||
|
vec operator + (const vec &a) const {vec b=(*this);b+=a;return b;}
|
||||||
|
vec operator - (const vec &a) const {vec b=(*this);b-=a;return b;}
|
||||||
|
vec operator * (float a) const {vec b=(*this);b*=a;return b;}
|
||||||
|
float norm(){return sqrt(x*x+y*y);}
|
||||||
|
}p[N];
|
||||||
|
|
||||||
|
const float XL=0.1; //左边框留白比例
|
||||||
|
const float XR=0.1; //右边框留白比例
|
||||||
|
const float YL=0.1; //上边框留白比例
|
||||||
|
const float YR=0.1; //下边框留白比例
|
||||||
|
const float vertex_R=.1; //点的半径
|
||||||
|
const float border_width=.01; //点的边框粗细
|
||||||
|
const string border_color="#616161"; //点的边框和边的颜色
|
||||||
|
const map<string,string> mp{{"b","#29B6F6"},{"r","#FF7043"}}; //颜色映射表
|
||||||
|
|
||||||
|
vec calc(vec a,vec b)
|
||||||
|
{
|
||||||
|
vec c=b-a;
|
||||||
|
c*=(vertex_R-border_width/2)/c.norm();
|
||||||
|
return a+c;
|
||||||
|
}
|
||||||
|
|
||||||
|
int n,m;
|
||||||
|
float minX,minY,maxX,maxY;
|
||||||
|
string pc[N];
|
||||||
|
|
||||||
|
void printhelp(const char* name)
|
||||||
|
{
|
||||||
|
printf(
|
||||||
|
"g2s the 6east svg graph generator, built on %s.\n"
|
||||||
|
"Usage: %s <inputfile> <outputfile>\n"
|
||||||
|
,__DATE__,name);
|
||||||
|
exit(1);
|
||||||
|
}
|
||||||
|
|
||||||
|
int main(int argc,char** argv)
|
||||||
|
{
|
||||||
|
if(argc!=3) printhelp(argv[0]);
|
||||||
|
freopen(argv[1],"r",stdin);
|
||||||
|
freopen(argv[2],"w",stdout);
|
||||||
|
cin>>n; //输入点数(int)
|
||||||
|
for(int i=1;i<=n;i++)
|
||||||
|
{
|
||||||
|
cin>>p[i].x>>p[i].y>>pc[i];
|
||||||
|
//输入第i个点的横坐标(float)、纵坐标(float)、半径(float)和颜色(string)
|
||||||
|
if(mp.find(pc[i])!=mp.end()) pc[i]=mp.find(pc[i])->second;
|
||||||
|
if(i==1) minX=maxX=p[i].x,minY=maxY=p[i].y;
|
||||||
|
if(p[i].x<minX) minX=p[i].x;
|
||||||
|
else if(p[i].x>maxX) maxX=p[i].x;
|
||||||
|
if(p[i].y<minY) minY=p[i].y;
|
||||||
|
else if(p[i].y>maxY) maxY=p[i].y;
|
||||||
|
}
|
||||||
|
minX-=vertex_R,minY-=vertex_R;
|
||||||
|
maxX+=vertex_R,maxY+=vertex_R;
|
||||||
|
float X=minX-(maxX-minX)*XL;
|
||||||
|
float Y=minY-(maxY-minY)*YL;
|
||||||
|
for(int i=1;i<=n;i++) p[i].x-=X,p[i].y-=Y;
|
||||||
|
X=(maxX-X)+(maxX-minX)*XR;
|
||||||
|
Y=(maxY-Y)+(maxY-minY)*YR;
|
||||||
|
cout<<"<?xml version=\"1.0\" encoding=\"UTF-8\"?>"<<endl;
|
||||||
|
cout<<"<svg xmlns=\"http://www.w3.org/2000/svg\" xmlns:xlink=\"http://www.w3.org/1999/xlink\" viewBox=\"0 0 "<<X<<" "<<Y<<"\" version=\"1.1\">"<<endl;
|
||||||
|
for(int i=1;i<=n;i++)
|
||||||
|
{
|
||||||
|
cout<<"<circle style=\"fill-rule:evenodd;fill:"<<pc[i]<<
|
||||||
|
";fill-opacity:1;stroke-width:"<<border_width<<
|
||||||
|
";stroke-linecap:square;stroke-linejoin:miter;stroke:"<<border_color<<
|
||||||
|
";stroke-miterlimit:"<<border_width*0.7<<
|
||||||
|
";\" cx=\""<<p[i].x<<"\" cy=\""<<p[i].y<<"\" r=\""<<vertex_R<<"\"/>"<<endl;
|
||||||
|
}
|
||||||
|
cin>>m; //输入边数(int)
|
||||||
|
for(int i=1;i<=m;i++)
|
||||||
|
{
|
||||||
|
int a,b;
|
||||||
|
cin>>a>>b; //输入端点编号(int[1,n])
|
||||||
|
vec A=calc(p[a],p[b]);
|
||||||
|
vec B=calc(p[b],p[a]);
|
||||||
|
cout<<"<path style=\"fill:none;stroke-width:"<<border_width<<
|
||||||
|
";stroke-linecap:butt;stroke-linejoin:miter;stroke:"<<border_color<<
|
||||||
|
";stroke-miterlimit:"<<border_width*0.7<<
|
||||||
|
";\" d=\"M "<<A.x<<" "<<A.y<<" L "<<B.x<<" "<<B.y<<" \"/>"<<endl;
|
||||||
|
}
|
||||||
|
cout<<"</svg>"<<endl;
|
||||||
|
return 0;
|
||||||
|
}
|
||||||
87
template.typ
Normal file
87
template.typ
Normal file
@ -0,0 +1,87 @@
|
|||||||
|
#let cnfont = ("Noto Sans CJK SC", "Noto Sans SC", "Source Han Sans CN")
|
||||||
|
#let cnmainfont = ("Noto Serif CJK SC", "Source Han Serif CN")
|
||||||
|
|
||||||
|
#let mtext(body) = text(font: cnmainfont, weight: "regular", body)
|
||||||
|
|
||||||
|
#let tab = h(2em)
|
||||||
|
#let halftab = h(1em)
|
||||||
|
|
||||||
|
#let footer_title = state("footer_title", "")
|
||||||
|
#let skip_footer = state("skip_footer", false)
|
||||||
|
|
||||||
|
#let thispage_number(loc) = {
|
||||||
|
let numberstarter = query(<PageNumberingStated>, before: loc)
|
||||||
|
if numberstarter == () {
|
||||||
|
none
|
||||||
|
} else {
|
||||||
|
loc.page() - numberstarter.first().location().page() + 1
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
#let problem_id = counter("pid")
|
||||||
|
|
||||||
|
#let project(title: "", logo: none, body) = {
|
||||||
|
set document(title: title)
|
||||||
|
set text(font: cnmainfont, lang: "zh")
|
||||||
|
set page(
|
||||||
|
width: 195mm,
|
||||||
|
height: 270mm,
|
||||||
|
margin: (top: 20mm)
|
||||||
|
)
|
||||||
|
|
||||||
|
show par: set block(above: 1.2em, below: 1.2em)
|
||||||
|
show heading: set text(font: cnfont, weight: "semibold")
|
||||||
|
set list(marker: (sym.square.filled.small, [--]), indent: .5em)
|
||||||
|
set ref(supplement: it => {
|
||||||
|
if it.func() == math.equation {
|
||||||
|
"式"
|
||||||
|
} else {
|
||||||
|
auto
|
||||||
|
}
|
||||||
|
})
|
||||||
|
|
||||||
|
set par(leading: 0.75em)
|
||||||
|
|
||||||
|
v(0.6fr)
|
||||||
|
if logo != none {
|
||||||
|
align(right, image(logo, width: 26%))
|
||||||
|
}
|
||||||
|
v(9.6fr)
|
||||||
|
|
||||||
|
text(4em, weight: "light", font: cnfont, title)
|
||||||
|
v(2.4fr)
|
||||||
|
|
||||||
|
pagebreak()
|
||||||
|
pagebreak()
|
||||||
|
|
||||||
|
outline(depth: 1)
|
||||||
|
[
|
||||||
|
#counter(page).update(1)
|
||||||
|
<PageNumberingStated>
|
||||||
|
#set page(footer: locate(loc => {
|
||||||
|
if skip_footer.at(loc) {
|
||||||
|
return
|
||||||
|
}
|
||||||
|
|
||||||
|
let thispage = thispage_number(loc)
|
||||||
|
let is_mainpart = query(<MainStarted>, before: loc) != ()
|
||||||
|
let is_mainpart = true
|
||||||
|
let footer_content = if is_mainpart {
|
||||||
|
[\##problem_id.at(loc).first() #footer_title.at(loc)]
|
||||||
|
}
|
||||||
|
|
||||||
|
let isleft = calc.even(thispage)
|
||||||
|
set align(left) if isleft
|
||||||
|
set align(right) if not isleft
|
||||||
|
if isleft { [#thispage] }
|
||||||
|
[ #halftab #underline(offset: 2pt, footer_content) #halftab ]
|
||||||
|
if not isleft { [#thispage] }
|
||||||
|
}))
|
||||||
|
|
||||||
|
// Main body.
|
||||||
|
#set par(justify: true)
|
||||||
|
#set text(15pt)
|
||||||
|
|
||||||
|
#body
|
||||||
|
]
|
||||||
|
}
|
||||||
Loading…
x
Reference in New Issue
Block a user